Queries about subdomain interface in L-Shape model

Contents

Summary of the demo

This demo is a comprehensinve illustration of MESH API for dealing with geometric and topological queries. In particular it shows:

Important remark

For the understanding of the demo it is important to keep in mind the fact that Mesh class provides in fact dual representation of the mesh. Both represenations are compatible but server somehow different purpses.

The first representation is build as the image of GMSH mesh file. It consist of three data structures for: nodes, elements and regions. The important fact is that if geometric domain defines regions of different dimension, that is phisical points, lines, surfaces or volumes, then the set of elements will also contain elements of different dimension. The will be segments, triangles, quads, tetrahedrons, hexahedrons and so on. It is important to note that all of them are called elements.

The second representation is base on a hierarchy of topological mesh entities. These entities are: vertices, edges, faces, cells. They are linked by incidence relations, that is vertices are bouding entities for edges, edges are bounding entities for faces, faces are bounding entities for cells. This topological representation is accessible as Adjacency objects. For instance:

e2v = mesh.getAdjacency(mp.Topo.Edge, mp.Topo.Vertex)

returns Adjacency object that for each edge lists the vertices belonging to the edge. Mesh class support all combination of first order adjacency relations. They are evaluated in lazy maner, that is they are calculated on the first request for them and stored for further use.

Mesh class provides methos to map one representation to the other, for instance to find to which element give face corresponds.

Geometric model with interface

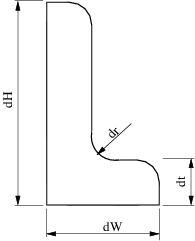
LShapeIfaceGeom class provides geometric model with internal boundary (called interface). The user can set the plcement of the interface with some restricted way by varying parameters fA and fB in the range (0, 1).

clear variables;

Create Mesher object

When Mesher object is created it takes care of initializing interface to GMSH mesh generator

mesher = mp.Mesher();

Create object describing geometric model

geom = mp.geoms.LShapeIfaceGeom('my_domain');
geom.params.dW = 3;
geom.params.dH = 4;
geom.params.dt = 1.5;

% Relative placement of interface endpoints.
geom.params.fA = 0.5;
geom.params.fB = 0.2;

% The mesh in the upper subdomain will consist of quad elements.
geom.params.quads = [0, 1];

Refine the mesh around interface

geom.setInterfaceLcFactor(0.5);

Generate mesh

mesh = mesher.generate(geom, struct('lc', 0.8));

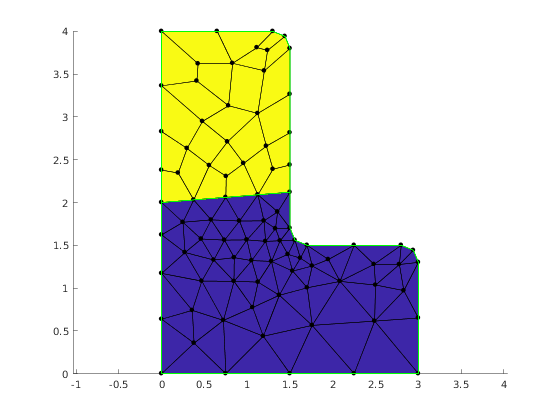
Visualize mesh

The simplest way to visualize mesh is to use Viewer class.

viewer = mp.Viewer();
viewer.show(mesh);

Report regions

mesh.printRegions();

         Region name |  ID | dim
--------------------------------
            b_bottom |   3 | 1
          b_left_top |   4 | 1
       b_left_bottom |   5 | 1
      b_other_bottom |   6 | 1
         b_other_top |   7 | 1
         i_interface |   8 | 1
         d_subBottom |   1 | 2
            d_subTop |   2 | 2

Accessing mesh entites on interface region

Getting interface region ID.

selector.name = {'i_interface'};
iID = mesh.findRegions(selector);
%
% Find Id of elements on interface.
iElems = mesh.findElems(struct('region', iID));

fprintf('Number of elements on interface: %d\n', length(iElems));

h = mp_plot_edges(gca, mesh.nodes, mesh.elements, struct('region', 6));
set(h, 'EdgeColor', 'red', 'LineWidth', 2);

edges = mesh.edgesFromElems(iElems);
viewer.labelEdges(edges);
viewer.stackFigure();
viewer.show(mesh);
viewer.labelEdges(struct('id',edges, 'labels',iElems));
viewer.labelElements(struct('asFaces', true));
inodes = mesh.elemNodes(iElems);
viewer.highlight_nodes(inodes);


e2f = mesh.getAdjacency(mp.Topo.Edge, mp.Topo.Face);

fprintf('\nName of regions adjacent to interface edges:\n')
for e = edges
  adjFaces = e2f.at(e);
  if length(adjFaces) ~= 2
    error('Interface edge has only one adjacen face');
  end
  r1 = mesh.getFaceRegion(adjFaces(1));
  r2 = mesh.getFaceRegion(adjFaces(2));
  fprintf('Edge %d  %20s %20s\n', e, mesh.getRegionName(r1), mesh.getRegionName(r2));
end

viewer.stackFigure();
viewer.show(mesh);

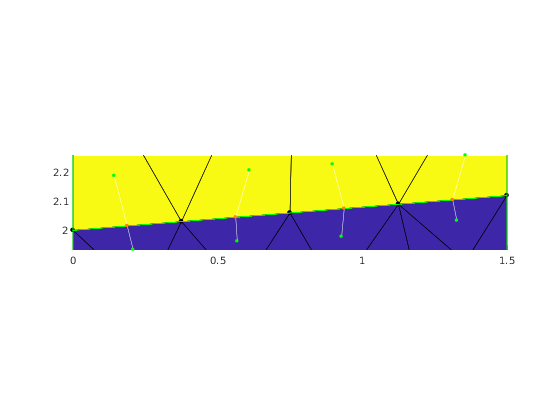
bbox = mp.BBox(mesh.nodes(inodes,:));

for e = edges
  adjFaces = e2f.at(e);
  pe = mesh.edgeCenters(e);
  pf1 = mesh.faceCenters(adjFaces(1));
  pf2 = mesh.faceCenters(adjFaces(2));
  showConnector(viewer, pf1, pf2, pe);
  bbox.update(pf1);
  bbox.update(pf2);
end
axis(bbox.extents);


viewer.stackFigure();
viewer.show(mesh);

nedges = length(edges);
% Preallocate arrays for tangent vectors, normal vectors, and anchor points
tan = zeros(2*nedges, 3);
nor = zeros(2*nedges, 3);
quiverPoint = zeros(nedges, 3);

% Fill the the arrays
k=0;
for e = edges
  adjFaces = e2f.at(e);
  for j=1:2
    [n, t] = mesh.csAtEdgeInFace(e, adjFaces(j));
    fc = mesh.faceCenters(adjFaces(j));
    ec = mesh.edgeCenters(e);
    quiverPoint(j+2*k, :) = ec+(ec-fc)*0.1;
    tan(j+2*k, :) = t;
    nor(j+2*k, :) = n;
  end
  k=k+1;
end
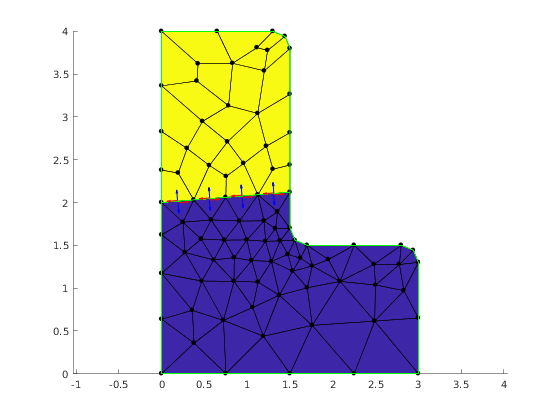
hold on;
quiver(quiverPoint(:,1), quiverPoint(:,2), tan(:,1), tan(:,2), 0.3, 'LineWidth', 1, 'Color', 'red');
quiver(quiverPoint(:,1), quiverPoint(:,2), nor(:,1), nor(:,2), 0.3, 'LineWidth', 1, 'Color', 'blue');

Number of elements on interface: 4

Name of regions adjacent to interface edges:
Edge 41           d_subBottom             d_subTop
Edge 81           d_subBottom             d_subTop
Edge 86           d_subBottom             d_subTop
Edge 44           d_subBottom             d_subTop

Internal management of demo

mp_manage_demos('report', 'LShapeIfaceGeom_queries', true);

Helper functions

function showConnector(viewer, pt1, pt2, pc)
  endsSpec = struct('PointSize', 10, 'Color', 'green');
  centerSpec = struct('PointSize', 10, 'Color', 'orange');
  viewer.showLine(pc, pt1, struct('Color', 'white'));
  viewer.showLine(pc, pt2, struct('Color', 'white'));
  viewer.showPoints(pt1, endsSpec);
  viewer.showPoints(pt2, endsSpec);
  viewer.showPoints(pc, centerSpec);
end

Published with MATLAB® R2017a